1 1 0 Binary Coding
Binary numbers based on 1s and 0s reflect the practical essence of computer hardware.
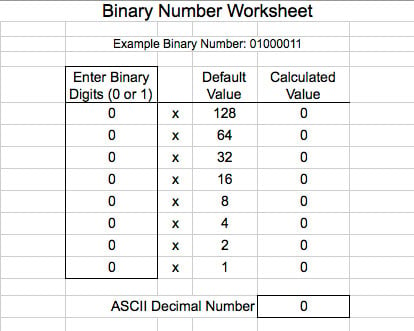
1 1 0 binary coding. A binary code represents text computer processor instructions or any other data using a two symbol system. To read binary numbers and convert them to their decimal equivalent you have two options. We get the value in the following manner.
Both off 0 first off second on 1 first on second off 2 both on 3 intermediate explanation another way of thinking about it is this. Any number can be represented by using these two digits i e. Refer to the example below for clarification.
0 0 0 0 1 1 1 0 1 1 1 0 carry over the 1 i e. Binary code takes each of those combinations and assigns a number to it like this. In short to convert binary numbers to decimal numbers you have to multiply each binary digit by two to the power of its place number from right to left and then add all the results together.
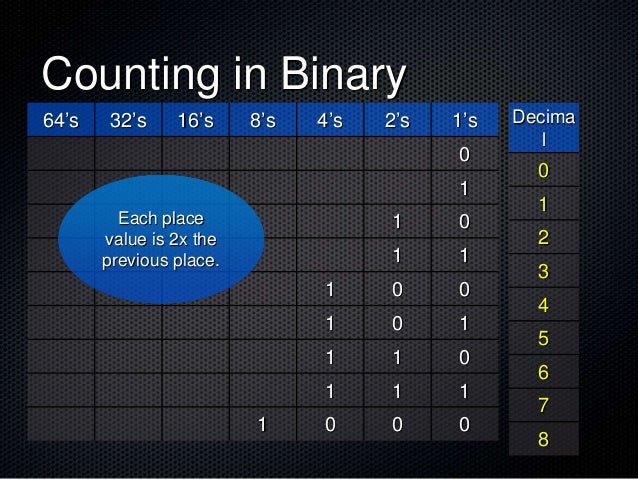
Electricity is either on or off. Like that we use only two digits to represent binary number. We use ten digits to represent a decimal number.
Here 4 digits are present in the sequence of digits 1 1 0 1. Note that in the binary system. Let s give each lightbulb a point value.
Decimal binary spelt 0. The two symbol system used is often 0 and 1 from the binary number system the binary code assigns a pattern of binary digits also known as bits to each character instruction etc for example a binary string of eight bits can represent any of 256 possible values and can. Binary addition follows the same rules as addition in the decimal system except that rather than carrying a 1 over when the values added equal 10 carry over occurs when the result of addition equals 2.
1111011001101111 0011100101011010 0010011100101011 1000011010000011 0010000010010011 1100110001011101 1001000100001100 0001001101011010 1001101101100100 1011110100001010.